Accelerating JavaScript arrays by 10x for Vector Search 🏹

You’ve probably heard about AI a lot this year. Lately, there’s been talk about something called Retrieval Augmented Generation (RAG). Unlike a regular chat with ChatGPT, RAG lets ChatGPT search through a database for helpful information. This makes the conversation better and the answers more on point.

Usually, a Vector Search engine is used as the database. It’s good at finding similar data points in a big pile of data. These data points are often at least 256-dimensional, meaning they have many Number-s. If you use JavaScript, you might wonder whether to use the built-in Array type or the more specialized TypedArray for this job.

In Python, we’ve seen up to a 300x speed difference handling these data points, depending on your tools. Now, let’s see how JavaScript stacks up.

Choosing Between Array and TypedArray?

The way TypedArray is set up is quite different from Array. It organizes data in a continuous memory buffer, similar to how C++’s std::vector operates. This setup allows the CPU to read values in sequence from the memory, using the CPU’s caches effectively. This should, in theory, lead to better performance. Well, that’s my hunch. Let’s put this to the test with a benchmark. We’ll create 1536-dimensional vectors akin to those churned out by OpenAI’s Ada “embeddings” API – a well-known solution ¹ to vectorize textual ² content.

1
2
3
4
5

const size = 1536;
const array1 = Array.from({ length: size }, () => Math.random());
const array2 = Array.from({ length: size }, () => Math.random());
const floatArray1 = new Float32Array(array1);
const floatArray2 = new Float32Array(array2);

To measure the performance of our arrays, we’ll compute the Cosine Distance between two vectors:

$$ \text{cosine distance}(A, B) = 1 - \frac{A \cdot B}{|A|_2 \times |B|_2} $$

The JavaScript implementation of the above formula:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

function cosineDistance(a, b) {
    let dotProduct = 0;
    let magA = 0;
    let magB = 0;
    for (let i = 0; i < a.length; i++) {
        dotProduct += a[i] * b[i];
        magA += a[i] * a[i];
        magB += b[i] * b[i];
    }
    return 1 - (dotProduct / (Math.sqrt(magA) * Math.sqrt(magB)));
}

This function computes the dot product of two vectors and normalizes it by their magnitudes. Once you’ve got benchmark installed with npm install benchmark, it’s time to set up the benchmark.Suite:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

import benchmark from 'benchmark';
const suite = new benchmark.Suite();
suite
    .add('Array of Numbers', () => {
        cosineDistance(array1, array2);
    })
    .add('TypedArray of Float32', () => {
        cosineDistance(floatArray1, floatArray2);
    })
    .on('cycle', (event) => {
        console.log(String(event.target));
    })
    .on('complete', () => {
        console.log('Fastest is ' + suite.filter('fastest').map('name'));
    })
    .run({
        noCache: true,
        async: false,
    });

I’ll use the c7g instances from the AWS Graviton3 family for the benchmarks. And here’s how our code fares:

Surprisingly, TypedArray trails behind Array by 3.4x! So much for optimization! Still, note that this comparison isn’t exactly apples to apples regarding memory usage; TypedArray is much more memory-efficient!

¹ While commercial endpoints offer robust solutions, there are equally powerful open-source feature-extraction models available on HuggingFace worth considering.

² Beyond text, vector representations can encapsulate various content types. For instance, Unum’s UForm specializes in vectorizing images.

Why is TypedArray Slow?

Heads up, we’re stepping into guesswork territory here. Though I’ve been a systems developer for a long time, my experience with JavaScript is barely a week in 20 years. But I have a hunch.

In the C++ world, there are std::vector and std::valarray. std::valarray was designed as a special array class for math operations, packed with “optimizations” for things like basic math, bit-level functions, exponentials, and trigonometry. But it didn’t catch on, and people talk about it more on StackOverflow than use it on GitHub. It becomes a hassle when speed isn’t a big deal and doesn’t deliver enough when speed is crucial. So it’s left on the shelf.

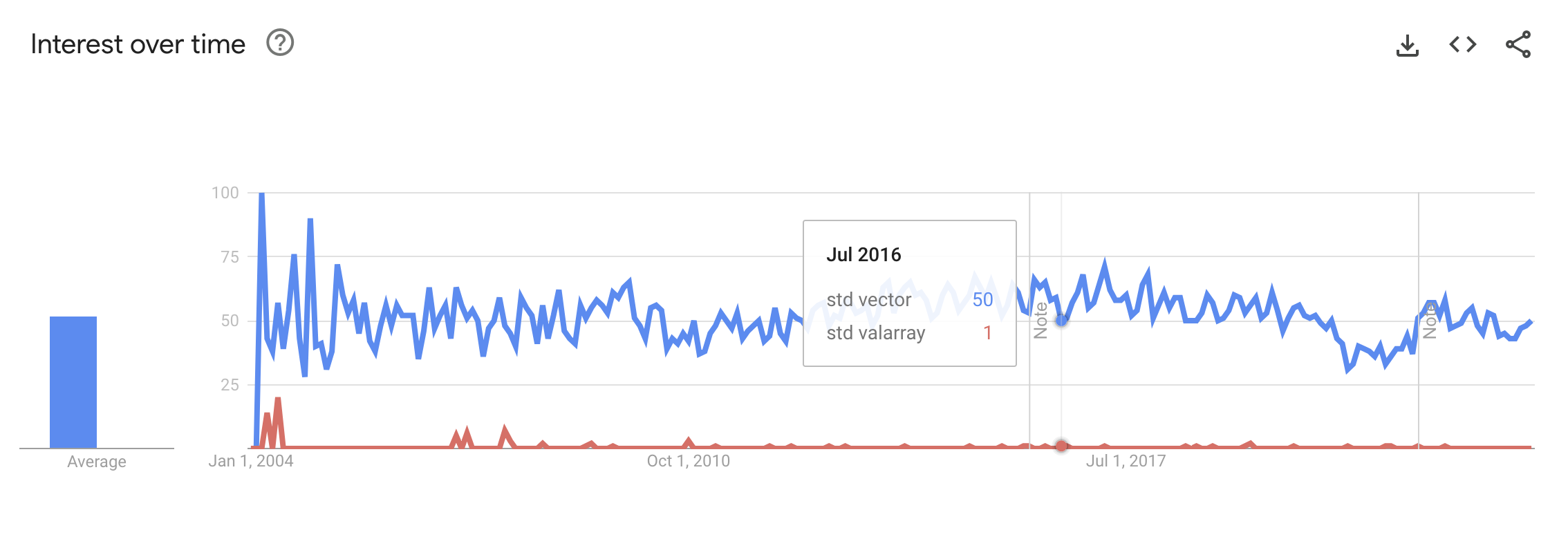
TypedArray in JavaScript seems to have a rougher time. It comes with zero math functions right off the bat, and its primary use is changing raw memory buffers into different types. With only a few developers using it, it seems like all the effort to make things run faster has been put into Array. So, what’s the point of TypedArray? Aside from using less memory, does it have anything else to offer?

Supercharging TypedArray

The TypedArray in JavaScript, much like Python’s “Buffer Protocol,” lets you dive into the underlying memory buffer as a straightforward byte array. This is handy when interacting with C/C++ libraries, precisely the route we’re taking here. Let’s rewrite the cosineDistance into pure C 99.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

#include <math.h> // for `sqrtf` implementation

float cosineDistance(float* a, float* b, int length) {
    float dotProduct = 0.0f;
    float magA = 0.0f;
    float magB = 0.0f;
    for (int i = 0; i < length; i++) {
        dotProduct += a[i] * b[i];
        magA += a[i] * a[i];
        magB += b[i] * b[i];
    }
    return 1.0f - (dotProduct / (sqrtf(magA) * sqrtf(magB)));
}

This code is almost identical to the JS variant, but we must expose it to Node. For that, one can use the NAPI. Every function in the binding gets 2 things:

• environment env for memory management and error handling,
• callback info for accessing the arguments.

The arguments are later parsed with napi_get_cb_info, unpacked from TypedArray using the napi_get_typedarray_info, and the result is converted back to JavaScript with napi_create_double. Putting it together:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#include <node_api.h>

napi_value cosineDistanceAPI(napi_env env, napi_callback_info info) {
    size_t argc = 2;
    napi_value args[2];
    napi_status status;

    // Get callback info and ensure the argument count is correct
    status = napi_get_cb_info(env, info, &argc, args, NULL, NULL);
    if (status != napi_ok || argc != 2) {
        napi_throw_error(env, NULL, "Wrong number of arguments");
        return NULL;
    }

    // Obtain the typed arrays from the arguments
    void *data_a, *data_b;
    size_t length_a, length_b;
    napi_typedarray_type type_a, type_b;
    napi_status status_a, status_b;
    status_a = napi_get_typedarray_info(env, args[0], &type_a, &length_a, &data_a, NULL, NULL);
    status_b = napi_get_typedarray_info(env, args[1], &type_b, &length_b, &data_b, NULL, NULL);
    if (status_a != napi_ok || status_b != napi_ok || type_a != type_b || length_a != length_b) {
        napi_throw_error(env, NULL, "Both arguments must be typed arrays of matching types and dimensionality");
        return NULL;
    }
    if (type_a != napi_float32_array) {
        napi_throw_error(env, NULL, "Only `float32` arrays are supported in JavaScript bindings");
        return NULL;
    }

    float result = cosineDistance(data_a, data_b, length_a);

    // Convert the result to a JavaScript number
    napi_value js_result;
    status = napi_create_double(env, result, &js_result);
    if (status != napi_ok)
        return NULL;

    return js_result;
}

napi_value Init(napi_env env, napi_value exports) {
    napi_property_descriptor cosineDesc = {"cosineDistance", 0, cosineDistanceAPI, 0, 0, 0, napi_default, 0};
    napi_define_properties(env, exports, 1, &cosineDesc);
    return exports;
}

NAPI_MODULE(NODE_GYP_MODULE_NAME, Init)

There’s no magic involved. Running the simple C 99 version against native JavaScript shows:

Our new C library is 10x faster than the JavaScript implementation over TypedArray, and 3x faster than the JavaScript implementation over Array! This is a vast improvement, but we can do better.

AI Doesn’t Need High Precision

JavaScript’s default Number type uses 64-bit double-precision floating point numbers. They’re precise but slow. Our TypedArray uses 32-bit single-precision floating point numbers, faster but still not fast enough. We can do better.

Many AI developers prefer 16-bit half-precision floating point numbers. However, JavaScript doesn’t support them. So, we’ll jump to 8-bit integers. I upscale numbers from 0 to 1 by 100 before changing them to integers.

1
2
3
4
5
6
7

const size = 1536;  
const array1 = Array.from({ length: size }, () => Math.random() * 100);
const array2 = Array.from({ length: size }, () => Math.random() * 100);
const floatArray1 = new Float32Array(array1);
const floatArray2 = new Float32Array(array2);
const intArray1 = new Int8Array(array1);
const intArray2 = new Int8Array(array2);

Here is the extended results table:

We got a 12% performance boost. It’s alright, but there might be specialized math libraries that can do better.

Trying MathJS and NumJS

MathJS and NumJS are well-known libraries with decent GitHub stars. MathJS is more popular with 650 K weekly downloads compared to NumJS’s 650. Yes, 1,000 times fewer downloads. Both are made in JavaScript, so they work well in the JS world but are slow.

When I saw those numbers, I ported my SimSIMD library to JavaScript. It provides CPU-specific implementations of math functions, like cosineDistance, using SIMD instructions. So, in some ways, SimSIMD is closer to Assembly than C. This may sound complex, but preparing the NPM module was a breeze. The whole binding took just 80 lines of C code and a trivial bindings.gyp config.

Do you use #NumPy or #SciPy to compute vector similarity? For @OpenAI Ada embeddings – SimSIMD does it 3-200x faster 🤯

float16 works great on every arch - Arm NEON & SVE and x86 AVX2 & AVX-512. Intel AMX also looks excellent 🔜https://t.co/ouFdvMJd7g#opensource #Python

— Ash Vardanian (@ashvardanian) October 5, 2023

Unlike other SIMD-accelerated libraries, it already supports both AVX-512 FP16 extensions on Intel Sapphire Rapids CPUs and Scalable Vector Extensions on the new 64-bit ARM Neoverse N2 cores in AWS Graviton3 instances. These instances are usually 30% cheaper, but with SimSIMD, you can get a 10x performance boost for free. Now, without leaving your JavaScript runtime, you can get performance most C++ and Rust applications don’t have 🎉

Taking Advantage of Multi-Threading

JavaScript runs on a single thread, but Node.js doesn’t. It has a thread pool for IO tasks and can use multiple threads for CPU-heavy work. The good news? Since we’re already working in C, we don’t need to worry about that 😅

In the C realm, you can pick any multi-threading library you like. A common choice is OpenMP, supported by many compilers. Instead of implementing parallel execution from scratch, we can take the USearch library for large-scale Vector Search. It uses SimSIMD for distance calculations and OpenMP to schedule the jobs. And just like SimSIMD, it has bindings for NodeJS. Let’s npm install usearch, and tweak our benchmark a bit:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

suite
    .add('2D Array of Numbers', () => {
        for (let i = 0; i < batchSize; i++) {
            for (let j = 0; j < batchSize; j++) {
                const start = i * dimensions
                const end = start + dimensions
                cosineDistance(matrix1.slice(start, end), matrix2.slice(start, end));
            }
        }
    })
    .add('2D TypedArray of Float32 with exact USearch', () => {
        usearch.exactSearch(floatMatrix1, floatMatrix2, dimensions, 1, MetricKind.Cos);
    })
    .add('2D TypedArray of Int8 with exact USearch', () => {
        usearch.exactSearch(intMatrix1, intMatrix2, dimensions, 1, MetricKind.Cos);
    })

Here are the results with a batchSize of 100 on just 4x vCPUs:

And with a batchSize of 1000 on the same 4x vCPUs:

This demonstrates the significant performance boosts you can achieve by leveraging multi-threading, especially when working with larger datasets.

Approximate Nearest Neighbors Search

Did you notice we used the exactSearch function from USearch? That’s because its default mode is “approximate”. USearch was initially designed to search across billions of points. But before you can search, you must “index” them. With the index set up, querying in it skips most distance computations - you might only compare a mere 0.0001% of the vectors in the dataset per request.

1
2
3
4
5

import usearch, { MetricKind } from 'usearch';

const index = new usearch.Index(dimensions, MetricKind.Cos);
index.add(keys, datasetMatrix);
results = index.search(queriesMatrix, 1);

The Index class implements a data structure called HNSW (Hierarchical Navigable Small World), a layered graph of points. It is somewhat similar to a Skip-List data structure or a hierarchical “cluster of clusters”… Unlike “a cluster of clusters”, HNSW handles boundary conditions much better when a point is far from centroids.

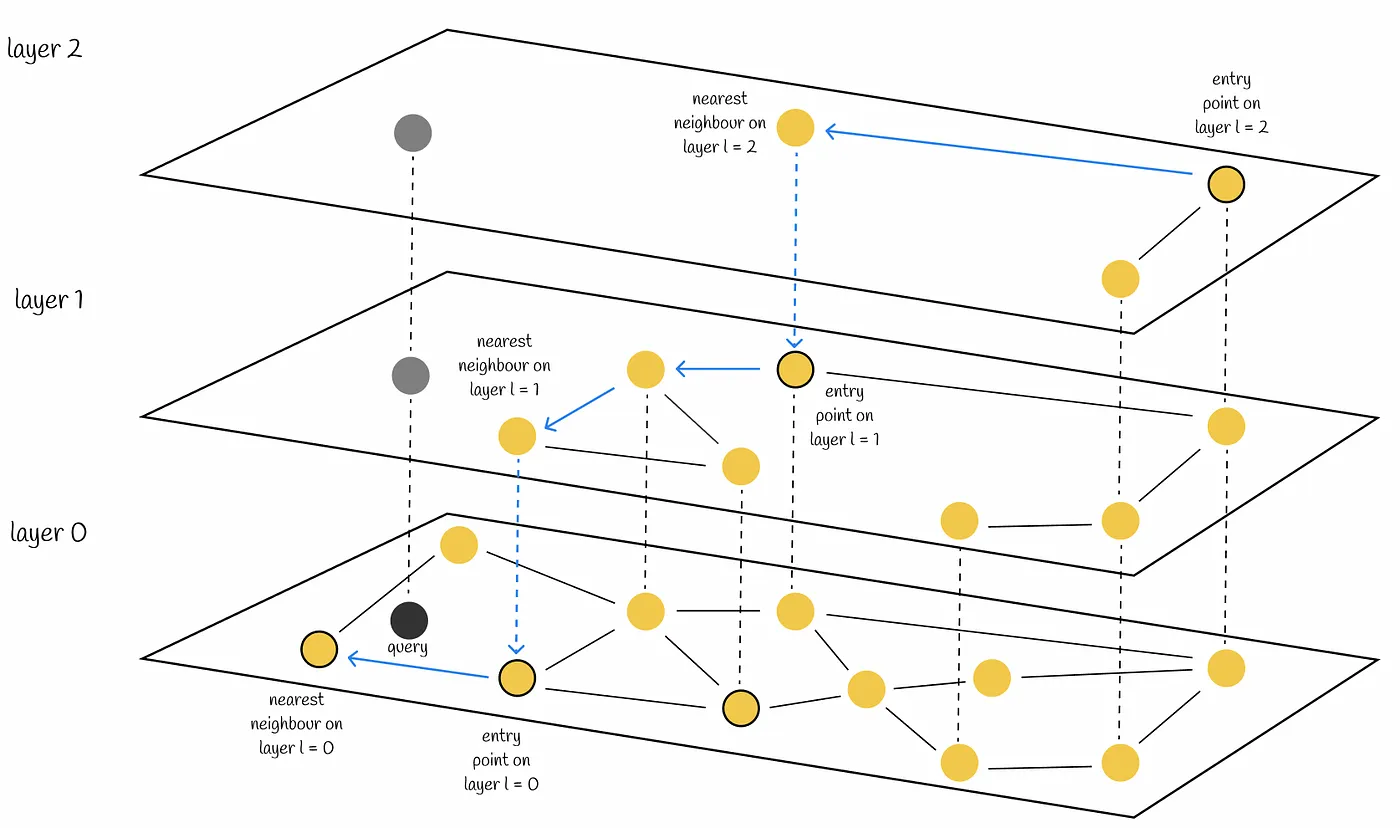
Other libraries, like Meta’s famous FAISS, use a similar structure. But thanks to better memory layout and SIMD-accelerated distance functions, USearch implementation seems much faster at scale and provides JavaScript bindings. USearch can sustain over 100,000 queries per second in our benchmark, even on a single machine. Intrigued?

1

npm install usearch simsimd

More on vector search:

• Abusing Vector Search for Texts, Maps, and Chess ♟️
• Stable Marriages in Economics, Dating, and Vector Search 💍
• SimSIMD: ≤ 200x faster SciPy distances with AVX-512 & SVE 📏