Vector Search is hot!
Everyone is pouring resources into a seemingly new and AI-related topic.
But are there any non-AI-related use cases?
Are there features you want from your vector search engine, but are too afraid to ask?
A few days ago, I built a new Vector Search engine - USearch.
Entirely open-source, Apache 2.0, free for commercial use.
It implements HNSW - “Hierarchical Navigable Small World” graphs, the most commonly used data-structure for Vector Search.
- It’s short - just 1000 lines of C++11.
- It’s fast - assuming high memory-locality and SIMD tricks.
- It’s compatible with Python, JavaScript, Java, Rust,
Go, and Wolfram.
Most importantly, USearch supports non-equidimensional vectors and custom similarity measures!
It’s a general-purpose data structure, limited only by your imagination and applicable to more than AI.
Let’s highlight some weird use cases and under-the-radar features.
Geo-Spatial Indexing#
When working with geospatial data, the most common representation is a combination of latitude and longitude.
One would use the Haversine formula to compute the distance between two points on a sphere.
USearch natively supports it.
So without further ado, I took a CSV with geo-locations of 140 thousand towns and districts from Kaggle and tried to find all the closest cities.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| from usearch import Index
import pandas as pd
import numpy as np
import geocoder
my_coordinates = np.array(geocoder.ip('me').latlng, dtype=np.float32)
df = pd.read_csv('cities.csv')
coordinates = np.zeros((df.shape[0], 2), dtype=np.float32)
coordinates[:, 0] = df['latitude'].to_numpy(dtype=np.float32)
coordinates[:, 1] = df['longitude'].to_numpy(dtype=np.float32)
labels = np.array(range(df.shape[0]), dtype=np.longlong)
index = Index(metric='haversine')
index.add(labels, coordinates)
matches, _, _ = index.search(my_coordinates, 10)
print(df.iloc[matches])
|
Sitting in a cafe in San Francisco, I received this.
1
2
3
4
5
6
7
8
9
10
11
| id name state_id state_code state_name country_id country_code country_name latitude longitude wikiDataId
128666 125809 San Francisco 1416 CA California 233 US United States 37.77493 -122.41942 Q62
128430 121985 Mission District 1416 CA California 233 US United States 37.75993 -122.41914 Q7469
127999 114046 City and County of San Francisco 1416 CA California 233 US United States 37.77823 -122.44250 Q13188841
127991 113964 Chinatown 1416 CA California 233 US United States 37.79660 -122.40858 Q2720635
128483 122925 Noe Valley 1416 CA California 233 US United States 37.75018 -122.43369 Q3342640
128864 128294 Visitacion Valley 1416 CA California 233 US United States 37.71715 -122.40433 Q495373
128049 115006 Daly City 1416 CA California 233 US United States 37.70577 -122.46192 Q370925
127926 112800 Brisbane 1416 CA California 233 US United States 37.68077 -122.39997 Q917671
128712 125970 Sausalito 1416 CA California 233 US United States 37.85909 -122.48525 Q828729
127927 112825 Broadmoor 1416 CA California 233 US United States 37.68660 -122.48275 Q2944590
|
Dataset.
Source.
Sto(n)ks#
We got lucky.
We were working with GIS data, and USearch has the Haversine metric bundled.
What if your metric of choice isn’t present?
Let’s imagine you are analyzing the stock market or the price change of a particular asset.
The first thing to do is to investigate which other assets follow the same trend.
In other words, which assets are covariant?
Covariance isn’t included.
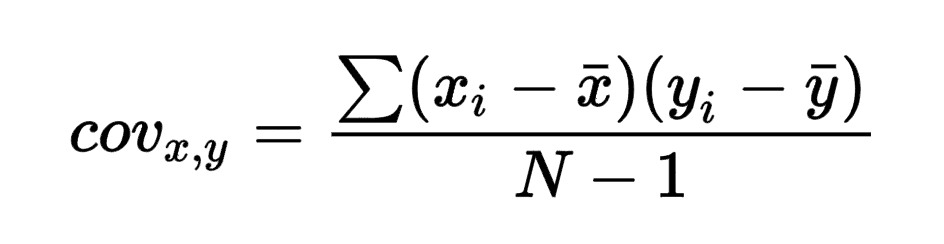
But once you check the formula, you realize it resembles the “Inner Product” metric.
If you have used FAISS, you know it doesn’t ship the angular distance, as it expects you to normalize vectors.
Same here.
We can pre-process the vectors, subtracting the np.mean, before passing to usearch.Index, and things will work.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| import os
import time
from statistics import covariance
from usearch import Index
import pandas as pd
import numpy as np
directory: str = 'stocks'
last_days: int = 30
tickets: list[str] = []
ticket_to_prices: dict[str, np.array] = {}
index = Index(ndim=last_days)
for filename in os.listdir(directory):
path = os.path.join(directory, filename)
ticket = filename.split('.')[0]
df = pd.read_csv(path)
prices_list = df['Close'][-last_days:].to_list()
prices = np.zeros(last_days, dtype=np.float32)
prices[-len(prices_list):] = prices_list
tickets.append(ticket)
index.add(len(index), prices - np.mean(prices))
ticket_to_prices[ticket] = prices
selected_ticker = 'AAPL'
tic = time.perf_counter()
selected_prices = ticket_to_prices[selected_ticker]
approx_matches, _, _ = index.search(
selected_prices - np.mean(selected_prices), 10)
approx_tickets = [tickets[match] for match in approx_matches]
toc = time.perf_counter()
print('Approximate matches:', ','.join(approx_tickets))
print(f'- Measurement took {toc - tic:0.4f} seconds')
tic = time.perf_counter()
covariances = [
(ticket, covariance(selected_prices, prices))
for ticket, prices in ticket_to_prices.items()]
covariances = sorted(covariances, key=lambda x: x[1], reverse=True)
exact_tickets = [ticket for ticket, _ in covariances[:10]]
toc = time.perf_counter()
print('Exact matches:', ','.join(exact_tickets))
print(f'- Measurement took {toc - tic:0.4f} seconds')
|
Running the script, we get a 2'000x performance improvement over the naive Python approach for a small collection of 5'884 entries covering a month of closing prices.
The benefits would be more significant with more extensive collections and longer ranges.
1
2
3
4
5
| Approximate matches: ELC, NVR, SEB, BKNG, MKL, TPL, CABO, TSLA, GOOGL, GOOG
- Measurement took 0.0001 seconds
Exact matches: ELC, NVR, MKL, TPL, CABO, AZO, BA, ISRG, FLGE, AMZN
- Measurement took 0.2396 seconds
|
Dataset.
Source.
Chess?!#
Imagine having to search through a database of chess positions.
There are specialized methods, often based on Zobrist hashing.
But there is also a more straightforward way.
A chessboard can be easily encoded with 64 bytes, where each byte encodes a particular piece.
1
2
3
4
5
| enum piece_t {
w_king_k, w_queen_k, b_king_k, b_queen_k,
w_pawn_k, w_rook_k, b_pawn_k, b_rook_k,
w_bishop_k, w_knight_k, b_bishop_k, b_knight_k,
};
|
You can compare two boards with a Hamming distance - index_gt<hamming_gt<piece_t>>.
Alternatively, you can design a custom scheme to weigh pieces differently, assuming pawns’ positions affect the game less than those of queens.
1
2
3
4
5
6
7
8
9
10
11
12
13
| unsigned weight(piece_t piece) {
switch (piece) {
case w_king_k: w_queen_k: b_king_k: b_queen_k: return 5u;
case w_rook_k: w_bishop_k: w_knight_k: b_rook_k: b_bishop_k: b_knight_k: return 3u;
default: return 1u;
}
}
struct position_distance_t {
unsigned operator () (piece_t const *board_a, piece_t const *board_b, std::size_t, std::size_t) const {
return std::transform_reduce(board_a, board_a + 64, board_b, 0u, std::plus {}, &weight);
}
};
|
This should also work for any other board or card game with discrete states, like Chess, Shogi, or Poker.
Text Search#
With LLMs and Socratic Models, Natural Language Processing is on the rise.
The go-to way of searching through texts is now embedding them with BERT, or something specialized, like ColBERT, and then putting outputs into a Vector Search engine: a modern representation and a modern index structure.
What if we combine an ancient representation with a modern index, retro-futuristically?
Tokens#
Typically, one would tokenize the text, pass it to the transformer, and then put the embedding into a Vector Search engine.
Still, one can compare the two texts by avoiding the intermediate step and intersecting the sets of present tokens to compute Jaccard similarity.
For that USearch has SetsIndex.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| from usearch import SetsIndex
from transformers import BertTokenizer
sets_index = SetsIndex()
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
def text2set(sample: str) -> np.array:
encoding = tokenizer.encode(sample, truncation=True)
encoding = encoding[1:-1]
encoding = sorted(set(encoding))
encoding = np.array(encoding, dtype=np.int32)
return encoding
sets_index.add(42, text2set('The answer to all your questions'))
|
Taking the HackerNews dataset and ~85K of its first entries, I’ve constructed an index and searched for theoretical physics.
1
2
3
4
5
6
7
| Results:
- 1. A science podcast you can try is Physics Frontiers. It gets pretty technical.
https://news.ycombinator.com/item?id=23588415
- 2. I wonder why exponentials are so common in nature/physics but tetration is not
https://news.ycombinator.com/item?id=32285985
- 3. Which is why of course physics departments pay you ~50% to do a PhD, whereas in Computer Science...
https://news.ycombinator.com/item?id=21440764
|
Probably not ideal, but it works!
Hashes#
Variable length representations aren’t always fast to work with.
If you know that the text will be having similar size, a common approach is to generate hash-like fingerprints.
For that USearch has HashIndex.
1
2
3
4
5
6
7
8
9
| from usearch import HashIndex
hash_index = HashIndex(bits=1024)
def text2hashes(sample: str) -> np.array:
words = sample.lower().split()
return np.array([hash(word) for word in words], dtype=np.int64)
hash_index.add(42, text2hashes('The answer to all your questions'))
|
This won’t give you high-quality search results.
Still, some companies would use a variation of that approach in complex multi-stage search pipelines.
Dataset.
Source.
Multi-Index Lookups#
Most Search systems operate on more than one embedding.
Imagine an online marketplace like Airbnb or Booking.
Once you open a listing, the platform will suggest a few alternatives.
It will search for nearby locations with similar pictures and textual descriptions.
Typically, geospatial indexing will be handled by a specialized system, but we can now put everything together.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| from usearch import Index
from uform import get_model
from ucall.rich_posix import Server
server = Server()
index_images = Index(ndim=256)
index_texts = Index(ndim=256)
index_coordinates = Index(metric='haversine')
model = get_model('unum-cloud/uform-vl-english')
@server
def recommend(text: str, image: Image, latitude: float, longitude: float) -> list[int]:
vector_image = model.encode_image(model.preprocess_image(image)).numpy()
vector_text = model.encode_text(model.preprocess_text(text)).numpy()
vector_coordinate = np.array([latitude, longitude], dtype=np.float32)
similar_images, _, _ = index_images.search(vector_image, 30)
similar_texts, _, _ = index_texts.search(vector_text, 30)
similar_coordinates, _, _ = index_coordinates.search(vector_coordinate, 100)
# If a listing is physically close and matches text or image, it must be first.
similar_contents = set(similar_images) + set(similar_texts)
return [label for label in similar_coordinates if label in similar_contents]
server.run()
|
Fused Embeddings#
When using mid-fusion models like UForm, you can get a multi-modal embedding out of the box.
Thus you can save one index lookup and still get more relevant results.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| index_contents = Index(ndim=384)
index_coordinates = Index(metric='haversine')
model = get_model('unum-cloud/uform-vl-english')
@server
def recommend(text: str, image: Image, latitude: float, longitude: float) -> list[int]:
vector_content = model.encode_multimodal(
image=model.preprocess_image(image),
text=model.preprocess_text(text)).numpy()
vector_coordinate = np.array([latitude, longitude], dtype=np.float32)
similar_contents, _, _ = index_contents.search(vector_content, 60)
similar_coordinates, _, _ = index_coordinates.search(vector_coordinate, 100)
# If a listing is physically close and matches contents, it must be first.
return [label for label in similar_coordinates if label in similar_contents]
|
JIT-ed User Defined Functions#
If you use a less specialized model, don’t worry.
You can concatenate the textual and image vector and customize the index to take your alternative similarity function.
In C++, it’s as easy as passing a custom template argument.
With Numba, however, you can get to the C++ layer without getting to the C++ layer.
Once you JIT-compile your function, you can pass it’s address to the C++ library like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| from numba import cfunc, types, carray
signature = types.float32(
types.CPointer(types.float32),
types.CPointer(types.float32),
types.size_t, types.size_t)
@cfunc(signature)
def metric(a, b, _, _):
a_array = carray(a, 512)
b_array = carray(b, 512)
text_similarity = 0.0
image_similarity = 0.0
for i in range(256):
image_similarity += a_array[i] * b_array[i]
text_similarity += a_array[i + 256] * b_array[i + 256]
return 2 - image_similarity - text_similarity
index_contents = Index(ndim=512, metric_pointer=metric.address)
@server
def recommend(text: str, image: Image, latitude: float, longitude: float) -> list[int]:
vector_image = model.encode_image(model.preprocess_image(image)).numpy()
vector_text = model.encode_text(model.preprocess_text(text)).numpy()
vector_content = np.concatenate((vector_image, vector_text))
similar_contents, _, _ = index_contents.search(vector_content, 60)
...
|
We have just built a composite recommendation system with zero microservices or dollars spent on private APIs.
The only thing left is to choose an excellent neural network tuned for your domain!
Which may not even be needed with the upcoming snapshots of UForm, promising better generalization across domains.
Not bad, right?
HNSW is a simple data structure, but unlike many older approaches, it has many applications.
That’s why we aren’t keen on quantization.
It takes away too many excellent properties.
That being said, we know that the core algorithm has space for improvement!
So feel free to fork it and try it yourself!
- USearch in-memory vector search 🔍
- UStore up to 10x faster multi-modal database 💾
- UForm tiny efficient multi-modal transformers 🧠
- UCall up to 100x faster networking ☎️
Don’t forget to star on GitHub 🤗 and reach out on Discord if you have any questions.